1、PID调节器基本原理及仿真研究
1.1 PID参数整定的基本方法
调节器PID参数整定方法可以分为时域整定和视屏整定两大类。时域方法中最基本的是Ziegler和Nichol提出的Z-N阶跃响应法。在实际的应用中传统的Z-N整定方法有着多种类型,最常见的有Cohen.Coon法和CHR法。其中CHR方法就是通过改变阶跃响应以得出较好的闭环特性的一种方法。
1.2 仿真实例
为了改善系统的性能,在系统中引入形如:
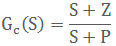 的串联校正网络,以改善系统的闭环极点。但是,Gc同时也会在系统闭环传递函数中增加一个新的零点。这个新增的零点肯定会严重影响闭环函数的动态性能。此时要考虑在系统的输入串接一个前置滤波器,以消除新增闭环零点的不利影响。
的串联校正网络,以改善系统的闭环极点。但是,Gc同时也会在系统闭环传递函数中增加一个新的零点。这个新增的零点肯定会严重影响闭环函数的动态性能。此时要考虑在系统的输入串接一个前置滤波器,以消除新增闭环零点的不利影响。设带有前置滤波器的控制系统乳图1所示,被控对象为
 ;校正网络为PI调节器,前置滤波器为
;校正网络为PI调节器,前置滤波器为 ;系统的设计主要为:①系统阻尼比为0.707;②阶跃响应的超调量≦5%;③阶跃响应的调节时间≦ 0.6s。
;系统的设计主要为:①系统阻尼比为0.707;②阶跃响应的超调量≦5%;③阶跃响应的调节时间≦ 0.6s。
图1 带前置滤波器的控制系统框图
试设计K1、K2及前置滤波器。
解:根据图1系统框图可得系统的闭环传递函数为
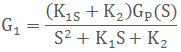 ;系统的闭环传递函数为
;系统的闭环传递函数为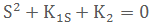
根据系统对阻尼比和调节时间的要求,令阻尼比为0.707,且由ts<0.6s
可求得ξWn≧7.33。取ξWn =8,故Wn=11.312.于是求出PI控制其参数为:
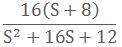 ;于是,无前置滤波器时,系统的上升时间为0.07s,峰值时间为0.2s,超调量为20.2%,调节时间为0.54s。显然,由于新增的零点的影响,超调量无法满足要求。
;于是,无前置滤波器时,系统的上升时间为0.07s,峰值时间为0.2s,超调量为20.2%,调节时间为0.54s。显然,由于新增的零点的影响,超调量无法满足要求。考虑采用前置滤波器Gp(s)来对消闭环传递函数中的零点,并同时保持系统原有的直流增益不变,为此取
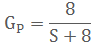 ;闭环传递函数变成
;闭环传递函数变成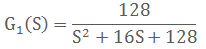
上升时间为0.29s,峰值时间为0.39s,超调量为4.3%,调节时间为0.55s
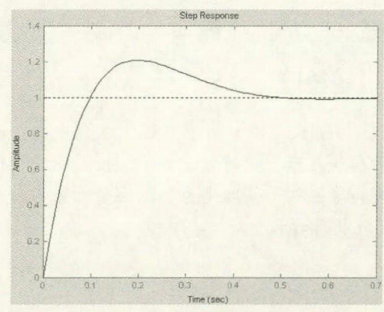
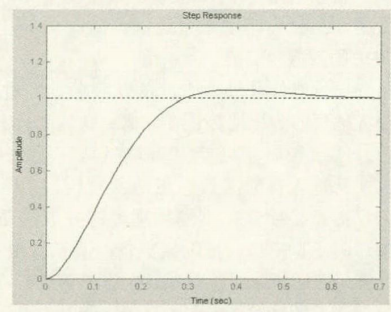
以上图形基于Z-N参数整定的方法来仿真的,根据设定函数的零极点,来抵消需要校正函数的零极点,从而达到设计的要求。此种方法简单、方便,通常用于要求精度不高的调节器中。
2、基于遗传算法的PID参数整定
2.1 遗传算法
2.1.1 编码与译码
遗传算法最常用的编码方法是二进制编码法,假设某一参数取值范围为[A,B],用长度h的二进制编码串来表示该参数,[A,B]将等分成2h-1个子部分,则它能产生2h种不同的编码。上述二进制编码所对应的编码公式为:
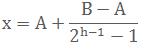 ,
, 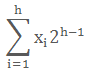
2.1.2 适应函数
为了体现染色体的适应能力而引入的对问题中的每一个染色体都能进行度量的函数叫适应度函数。通过适应度函数来决定染色体的优劣程度,它体现了自然进化中的优胜劣汰原则。
2.1.3 选择
选择又称为复制,是在群体中选择生命力强的个体产生下一代群体的过程。遗传算法使用选择算子来对种群中的个体进行选择操作;根据每个个体的适应度大小来进行选择适应度高的被遗传到下一代的概率较大,适应度小的被遗传到下一代的概率就小。选择操作的目的是为了避免有用的遗传信息的丢失,提高全局收敛性和计算效率。确定一个好的选择算子,能提高搜索的全局性,避免早熟。
2.1.4 交叉、变异
基本的遗传操作主要由3种:选择、交叉、变异。选择操作也叫复制操作,根据个体适应度函数值所度量的优劣程度决定它在下一代是被淘汰还是被遗传。一般地说,选择将使适应度较大的个体有较大的存在机会,而适应度较小的个体继续存在机会也较小。
2.2 遗传算法对PID参数整定的实例
PID调节器的三个参数Kp、Ki、Kd进行二进制编码,其中Kpϵ(0.1,20),Kiϵ(0,2),Kdϵ(0,2)每个参数的长度取14为,3个参宿一次串接,形成一个个体,个体长度为L=42,种群大小取n=30.选择算法采用常用的赌轮算法。交叉概率一般取0.4-0.9,本实例中取Pc=0.7,变异概率取0.0001-0.1,本实例Pc=0.01,收敛代数取迭代300次结束。遗传算法寻优得:Kp=4.8651,Ki=0.4252,Kd=0.6355
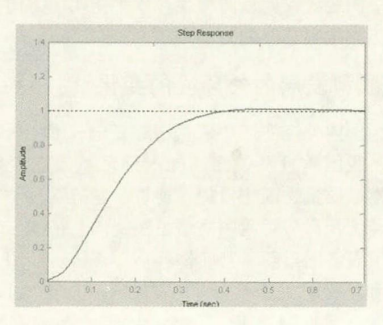
上升时间:0.50s;超调量为1.23%
遗传算法对于多变、目标函数不可微或不确定问题解的寻优,比传统的优化方法有更广泛的适应性。仿真结果表明遗传算法应用于PID调节器参数优化方法。
智能控制的发展日新月异,结合调节器新的控制算法,例如神经网络、遗传算法、专家控制方式等,把它们运用到传统PID控制中,已获得适应非线性、时变不确定性,并于难以建立精确的数学模型的复杂控制环境中获得大大优化于传统PID控制的动态性能和稳态性能;像遗传算法和PID相结合的自适应PID控制以及模糊神经网络和PID相结合的PID控制方式都是研究的重要方向。
PID调节器因为结构简单、容易实现,并且具有较强的鲁棒性,因而被广泛应用于各种工业过程控制中。尽管已经出现多种先进控制方法,PID控制仍然在各种工业控制技术中占据主导地位。PID调节器参数整定优劣与否,是以其能否在实用中得到好的闭环控制效果为前提条件的。迄今为止,各种先进PID调节器参数整定方法层出不穷,但在实际应用中,这些先进的整定方法并没有像预期的那样产生完美的控制效果。这主要是因为PID调节器结构上的简单性决定了它在控制品质上的局限性,并且这种简单性使得PID调节器对大时滞、不稳对象等被控对象的控制性能不是很好,同时PID调节器无法同时满足对设定值跟踪和抑制外扰的不同性能要求。本文提出的遗传算法在一定程度上改进了PID调节器性能指标。







