
傅里叶级数就是这样的一个例子。约瑟夫·傅里叶(Joseph Fourier)是一位19世纪的法国数学家,他对热如何在物体中流动很感兴趣。他的第一个贡献是现在称为热方程的公式,也是一个偏微分方程的例子,它描述了物体的温度T如何随时间t和空间x变化。用现代符号表示,热方程如下:
其中k是物体的热导率,这个数值衡量了物体传导热量的能力。
如果你能找到这个方程的解,它会告诉你物体在每个点x和时间t的温度T(x,t)。
傅里叶的第一个非凡想法是,他可以通过将T(x,t)表示为简单函数的和来解热方程,然后用这些函数来找到解。就好比分块砌砖盖房子比一次性盖房子要容易得多。
他的第二个非凡的想法在于他选择了哪些函数来构建温度。他选择了在三角学(研究三角形)中出现的正弦和余弦函数,因此他写下了T的表达式:
这个和式是无穷的,
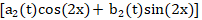 后的下一个项是
后的下一个项是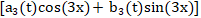 ,
,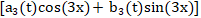 后的再下一个是
后的再下一个是 ,以此类推。
,以此类推。其中a0(t)、a1(t)、a2(t)等等和b1(t)、b2(t)、b3(t)等等都是系数,其具体值取决于初始条件。这种表达式现在被称为傅里叶级数。
乍一看,这种表示T的方法很不一般。毕竟,三角形和热流之间可能有什么联系呢? 然而,这正是解决上述热方程的正确选择。它使问题分解为一组更简单的问题,每个问题都可以单独解决,然后组合起来找到原问题的解。
事实上,在傅里叶最初的想法提出之后不久,人们发现用正弦和余弦来构建函数也可以解决许多其他问题,包括描述波的运动、气体的行为、许多重力问题、电静力学、电磁学、仪表,甚至股市行为的问题。
在傅里叶发现傅里叶级数之后,许多数学家开始致力于扩展和推广他的思想,并在此过程中发现了许多美妙的结果,包括一个巧妙的推导公式(最初由莱昂哈德·欧拉发现):
傅里叶级数及其在计算机上的离散推广在现代技术中起着基础性的作用。特别是我们用它们来合成和处理声音、信息和图像,音乐、电视、视频产业和仪表领域的存在都离不开傅里叶级数。







