在查阅了大量的资料后,电力仪表整理出了一个关于在目标温度下电线承载电流的两种计算方法供大家参考。
方法一:参考EIA 214标准进行某个固定温度时电线能承载电流计算
本方法是参考EIA 214标准进行了整理和总结,并且参考了论文Continuous Current and Temperature Rise in Aircraft Cables, M.Schach, AIEE Transactions, Part II, volume 71.
一、本文所推荐的计算方法适用于下列条件
1、电流可以是直流电或交流电,交流电可以是单相的,也可以是多相的,频率可以达到最高800Hz,超过800Hz的,要考虑交流阻抗和肌肤效应。
2、电线的绝缘皮在空气中的主要散热方式是对流和辐射。在每次计算时必须要确定特定的环境条件,例如海拔高度、环境空气温度、对流类型等。
3、电线结构
电线导体截面积;电线导体的材料,实心或绞合的。如果是绞合的,导体应该形成一个紧凑的圆形单元;电线的导体绝缘层,与导体同心,有可能是一层的,也有可能是多层不同材料的。
二、基本原理
在热平衡条件下,导体产生热量的功率(电流的平方乘以导体电阻)等于热量通过绝缘体的传导功率。也等于热量从电线绝缘皮外部对流和辐射到周围空气或墙壁的功率。电流的计算是通过用图解法同时求解这二个公式的交点得到的:①热量从导体向绝热体的传导;②从绝热体表面对流和辐射到周围环境。
三、符号定义
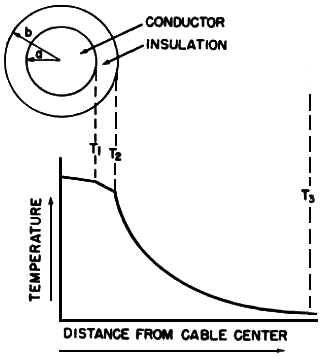
T1:电线导体的目标温度;
T2:绝缘皮外表面的温度;
T3:环境空气温度;
I:电流;
RT1:温度T1时导体单位长度的电阻;
P:12RT1;
a:导体的实际直径;
b:绝缘的实际外径;
K:绝缘材料的热传导率;
h:自然对流系数;
r:辐射系数;
T2K:绝缘表面的绝对温度,1K=C+273;
T3k:环境的绝对温度;1K=C+273;
e:绝缘表面的辐射率;
S:斯特藩-玻尔兹曼(Stefan-Boltzmann)常数=37.0×10-12W×inch-2(K)-4
各参数的值
自然对流系数h的单位是W×inch-2℃-1。绝缘表面的辐射率e的值应该由电线绝缘材料的厂家提供,在厂家没有提供的情况下,一般取0.9。
绝缘材料的导传热率K值也应该由制造供应商提供,在厂家没有提供的情况下,一般取3.5×10-4(Calorie×cm-1℃-1 )或 3.7×10-3(W×inch-1*℃-1)
特定温度(T1)下的导体电阻值RT1可以从导线中测量或计算,例如,参照标准ASTM B193电导体材料电阻率的标准试验方法和ASTM B286电子设备连接线用铜导线标准规格。
环境温度T3以及其他二个温度T1和T2如下图1所示。
辐射系数r的值由下列关系式计算得到。一般
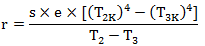
四、电流I的计算步骤
在导体目标温度T1确定的情况下 ,T1-T3就是目标温升。但是由于电线绝缘皮会传导热量,所以电线表面的温度T2并不等于T1, 是一个比T1小一些的未知量。
计算的目的就是要找到热量平衡时的T2值。
再次强调:电流的计算是通过用图解法同时求解这二个公式的交点得到的:①热量从导体向绝热体的传导;②从绝热体表面对流和辐射到周围环境。
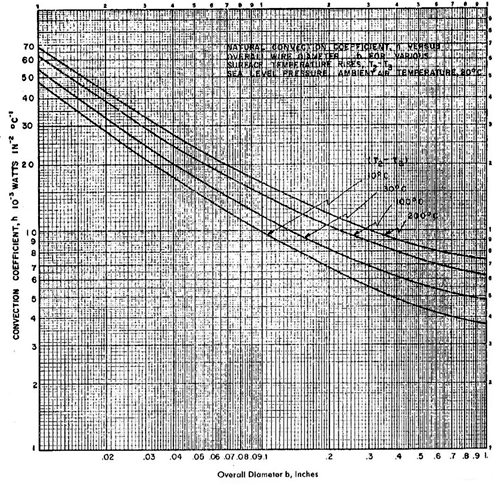
在以下的步骤中,除了功率P和绝缘的外表面温度T2外,其他的参数都是已知的。这些已知的参数包括T1、T3、K、e、b、a和RT1,然对流系数h值是通过图2查到的,图2是来自于w. Elenbaas的对流曲线(W. Elenbaas, "Dissipation of Heat by Free Convection", Phillipe Research Report&, 1948, p358)。
辐射系数r的值由等式1计算得到。
第一步,电缆中单位长度的热量在导体中产生并通过绝缘层向外按径向传导的功率由等式2给出。根据下面等式2,绘制出P与T2的关系曲线,这个是电线导体产生的热量功率。
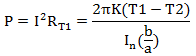
第二步,单位长度电线通过对流从电缆外表面向外传导热量的功率可以表示为等式3,
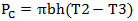
单位长度的电缆向外辐射热量的功率可以表示为等式4,
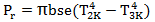
用r值替代掉等式4中的一些参数,则单位长度电缆从外表面向外界传输热量的总功率变为等式5,
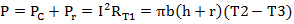
最后根据等式5,再绘制出另一个P与T2的关系曲线,这个是电线的绝缘皮向外传导的热量功率。
根据第1步和第2步的曲线,找到P值的交点,其就是导体期望温升(T1-T3)下,T2温度对应的P值。这个P值的交点意味着导体产生的热量等于绝缘皮向外散发的热量。
第三步,根据等式6,和已知的RT1值,计算出电流值I。
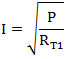
五、额定电流的一个计算例子
给定一个UL1007,16AWG的电线
a=0.0566inch(电线的近似导体直径)
b=0.0906inch (电线绝缘直径)。
T1=38℃,T3=20℃,此时电线导体的目标温升为38-20=18度。
K=3.7×10-3(W*inch-1*℃-1)
RT1=0.337×10-3Ω*inch-1(T1温度时的电阻)
第一步,根据等式2,计算出P与T2的关系式, 单位是W。
第二步,根据等式5,计算P与T2的另一个关系式,单位是W
参数h可以由图2查到,参数r可以由等式1计算得到。未知量是T2, 由于T2的可能值是比T1略小一些的值,所以,可以在一个小的范围内针对不同的T2温度,查到h值,计算r值和P值。计算结果如下表所示。
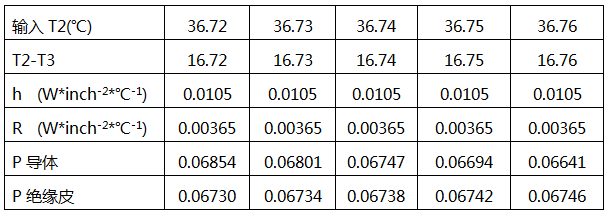
P值与T2的关系曲线如图3所示。两条曲线的交点值为T2=36.741度 , P=0.0674W,这个就是导体产生的热量和绝缘皮能传导的热量平衡时的P值。
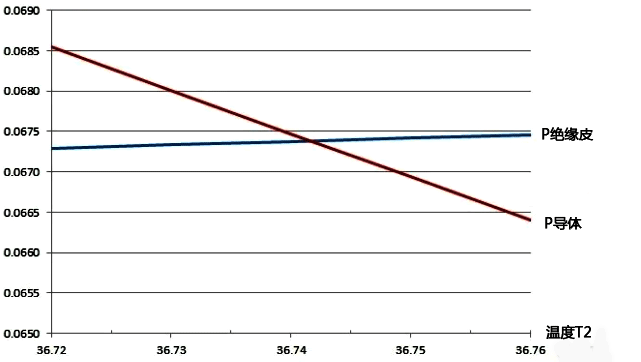
第三步,根据等式6,计算出电线能承载的电流。求得 I=14.1(A)
五、推广
用相同的方法,经过计算和分析,得到不同温升时的电流结果,并整理成一个指数表达式为:
电线导体温升11度时,I=9.17×(A)^0.6256,其中A为电线的截面积,单位是平方毫米,电流单位为安培。
电线导体温升18度时,I=11.96×(A)^0.6254,其中A为电线的截面积,单位是平方毫米,电流单位为安培。
电线导体温升30度时,I=15.63×(A)^0.625,其中A为电线的截面积,单位是平方毫米,电流单位为安培。
电线导体温升50度时,I=20.22×(A)^0.6263,其中A为电线的截面积,单位是平方毫米,电流单位为安培。
经过分折得出,电线绝缘直径的变化对电流的影响在很小的百分比范围内。
六、电流参考
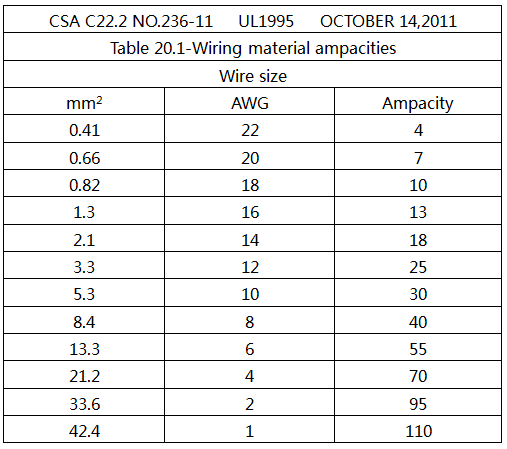
查找了UL1995标准-加热和制冷设备相关要求,在这个标准中的表20.1有定义了连接电线的电流值,如图4所示。这个值与上面第五部分所推导出的电线导体温升18度时的公式计算出的电流值是很接近的。
方法二:参考EIA 214标准进行某个固定温度时电线能承载电流计算
最近研究了一下日本标准JASO D609,这个标准中列出了很多汽车用电线的承载电流能力,也给了一个简单的计算方法。经过研究对比,发现其结果与EIA 214是很接近的。现在把JASO D609的方法在这里介绍一下。
用到的公式和参数如下:
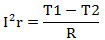
公式中:I为电缆载流量(A);r为导体电阻;T1为电缆最大工作温度;T2为环境温度(℃);R为热阻(℃.cm/W)
此外,在T1℃导体电阻rT1根据下式计算:
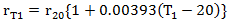
这里:r20为20℃下的导体电阻(单位:Ω/cm)
R=R1+R2
这里:R1为绝缘材料热阻(℃.cm/W);R2为表面接触热阻(℃.cm/W)
绝缘材料热阻:
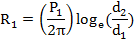
这里:P1为绝缘材料热阻率(℃.cm/W),聚氯乙烯取600,聚乙烯取450;d1为导体外径;d2为绝缘外径
表面接触电阻率

这里:P2为电缆表面接触热阻(℃.cm/W);当d2≤12.5mm,P2=300+32d2;d2>12.5mm,P2=700
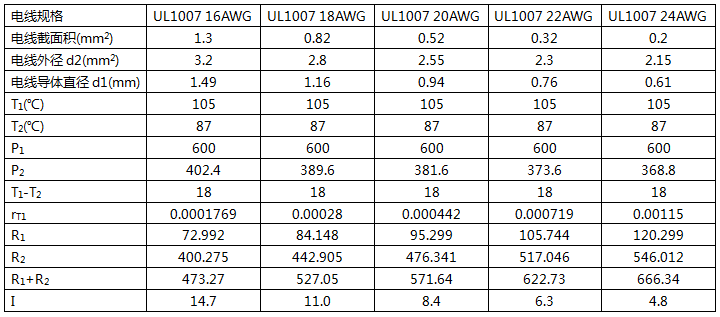
现在以UL 1007电线为例,进行计算。UL1007电线的规格如下。
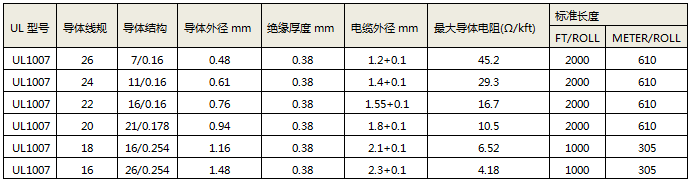
我们先以温升18度时的电流进行计算。由于JASO D609的计算公试是以最高工作温度减去环境温度的方法来表示温升的。所以,我们设定UL1007电线的最高工作温度是80度,环境温度为62度,此时,最大温升为18度时的电流承载能力如下表。
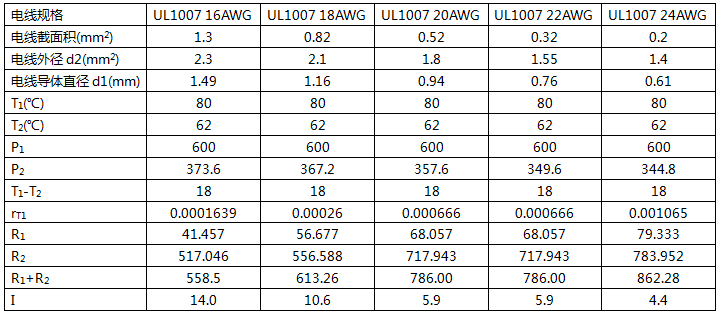
依据同样方法,计算出UL1015标准的电线的承载电流能力。在相同线规情况下,UL1015电线的导体直径同UL1007的差不多,但绝缘直径UL1015要比UL1007大0.76~0.8mm。UL1015电线的额定工作温度是105度。计算结果如下表所示。
依据同样方法,计算出温升30度和温升50度时电线承载电流情况。并且把根所EIA 214推导出来的电线承载电流的计算公式进行比较,得到如下表。
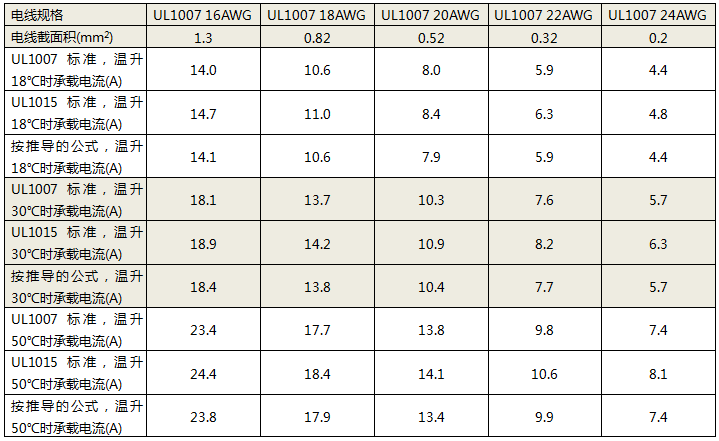
从上表可以看出,对于UL1007和UL1015电线,绝缘皮壁厚分别为0.38和0.76,在电线面积相同的情况下,电线的承载能力相差在1A以内。其他标准的电线也差不多在这个厚度区间范围内,而用EIA 214推导公试计算出来的电流值处于计算结果接近于绝缘皮壁厚在0.38mm时的结果。下面再次把根据EIA 214推导出来的,电线的任一面积的电流承载公试列出如下:
电线导体温升11度时,I=9.17*(A)^0.6256,。
电线导体温升18度时,I=11.96*(A)^0.6254。
电线导体温升30度时,I=15.63*(A)^0.625。
电线导体温升50度时,I=20.22*(A)^0.6263。
其中A为电线的截面积,单位是平方毫米。电流单位为安培。
在温升某个固定温度时电线承载电流的两种计算方法就分享到这里,希望对大家有所帮助。
作者:陆明超
相关阅读
最全电线载流量对照表
导线载流量估算口诀及解释







